考作诗考小品 艺术院校校考频现“奇题”选人才

"Tree search" redirects here; not to be confused with Search tree.

百度 甚至有HR爆料，工作几年就可以退休了。

In computer science, tree traversal (also known as tree search and walking the tree) is a form of graph traversal and refers to the process of visiting (e.g. retrieving, updating, or deleting) each node in a tree data structure, exactly once. Such traversals are classified by the order in which the nodes are visited. The following algorithms are described for a binary tree, but they may be generalized to other trees as well.

Types

A

B

C

D

E

F

0

Traversal method: 1

Previous node Restart Start

An interactive demonstration of different tree traversal methods

Unlike linked lists, one-dimensional arrays and other linear data structures, which are canonically traversed in linear order, trees may be traversed in multiple ways. They may be traversed in depth-first or breadth-first order. There are three common ways to traverse them in depth-first order: in-order, pre-order and post-order. Beyond these basic traversals, various more complex or hybrid schemes are possible, such as depth-limited searches like iterative deepening depth-first search. The latter, as well as breadth-first search, can also be used to traverse infinite trees, see below.

Data structures for tree traversal

Traversing a tree involves iterating over all nodes in some manner. Because from a given node there is more than one possible next node (it is not a linear data structure), then, assuming sequential computation (not parallel), some nodes must be deferred—stored in some way for later visiting. This is often done via a stack (LIFO) or queue (FIFO). As a tree is a self-referential (recursively defined) data structure, traversal can be defined by recursion or, more subtly, corecursion, in a natural and clear fashion; in these cases the deferred nodes are stored implicitly in the call stack.

Depth-first search is easily implemented via a stack, including recursively (via the call stack), while breadth-first search is easily implemented via a queue, including corecursively.

Depth-first search

Main article: Depth-first search

Depth-first traversal (dotted path) of a binary tree:

• Pre-order (node visited at position red ●):
      F, B, A, D, C, E, G, I, H;
• In-order (node visited at position green ●):
      A, B, C, D, E, F, G, H, I;
• Post-order (node visited at position blue ●):
      A, C, E, D, B, H, I, G, F.

In depth-first search (DFS), the search tree is deepened as much as possible before going to the next sibling.

To traverse binary trees with depth-first search, perform the following operations at each node:

1. If the current node is empty then return.
2. Execute the following three operations in a certain order:

   N: Visit the current node.

   L: Recursively traverse the current node's left subtree.

   R: Recursively traverse the current node's right subtree.

The trace of a traversal is called a sequentialisation of the tree. The traversal trace is a list of each visited node. No one sequentialisation according to pre-, in- or post-order describes the underlying tree uniquely. Given a tree with distinct elements, either pre-order or post-order paired with in-order is sufficient to describe the tree uniquely. However, pre-order with post-order leaves some ambiguity in the tree structure.

There are three methods at which position of the traversal relative to the node (in the figure: red, green, or blue) the visit of the node shall take place. The choice of exactly one color determines exactly one visit of a node as described below. Visit at all three colors results in a threefold visit of the same node yielding the “all-order” sequentialisation:

F-B-A-A-A-B-D-C-C-C-D-E-E-E-D-B-F-G-G-?I-H-H-H-?I-?I-G-F

Pre-order, NLR

1. Visit the current node (in the figure: position red).
2. Recursively traverse the current node's left subtree.
3. Recursively traverse the current node's right subtree.

The pre-order traversal is a topologically sorted one, because a parent node is processed before any of its child nodes is done.

Post-order, LRN

1. Recursively traverse the current node's left subtree.
2. Recursively traverse the current node's right subtree.
3. Visit the current node (in the figure: position blue).

Post-order traversal can be useful to get postfix expression of a binary expression tree.

In-order, LNR

1. Recursively traverse the current node's left subtree.
2. Visit the current node (in the figure: position green).
3. Recursively traverse the current node's right subtree.

In a binary search tree ordered such that in each node the key is greater than all keys in its left subtree and less than all keys in its right subtree, in-order traversal retrieves the keys in ascending sorted order.

Reverse pre-order, NRL

1. Visit the current node.
2. Recursively traverse the current node's right subtree.
3. Recursively traverse the current node's left subtree.

Reverse post-order, RLN

1. Recursively traverse the current node's right subtree.
2. Recursively traverse the current node's left subtree.
3. Visit the current node.

Reverse in-order, RNL

1. Recursively traverse the current node's right subtree.
2. Visit the current node.
3. Recursively traverse the current node's left subtree.

In a binary search tree ordered such that in each node the key is greater than all keys in its left subtree and less than all keys in its right subtree, reverse in-order traversal retrieves the keys in descending sorted order.

Arbitrary trees

To traverse arbitrary trees (not necessarily binary trees) with depth-first search, perform the following operations at each node:

1. If the current node is empty then return.
2. Visit the current node for pre-order traversal.
3. For each i from 1 to the current node's number of subtrees ? 1, or from the latter to the former for reverse traversal, do:
   1. Recursively traverse the current node's i-th subtree.
   2. Visit the current node for in-order traversal.
4. Recursively traverse the current node's last subtree.
5. Visit the current node for post-order traversal.

Depending on the problem at hand, pre-order, post-order, and especially one of the number of subtrees ? 1 in-order operations may be optional. Also, in practice more than one of pre-order, post-order, and in-order operations may be required. For example, when inserting into a ternary tree, a pre-order operation is performed by comparing items. A post-order operation may be needed afterwards to re-balance the tree.

Breadth-first search

Level-order: F, B, G, A, D, I, C, E, H.

Main article: Breadth-first search

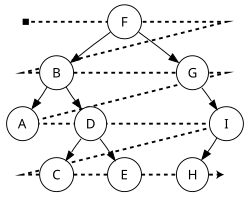
In breadth-first search (BFS) or level-order search, the search tree is broadened as much as possible before going to the next depth.

Other types

There are also tree traversal algorithms that classify as neither depth-first search nor breadth-first search. One such algorithm is Monte Carlo tree search, which concentrates on analyzing the most promising moves, basing the expansion of the search tree on random sampling of the search space.

Applications

Tree representing the arithmetic expression: A * (B ? C) + (D + E)

Pre-order traversal can be used to make a prefix expression (Polish notation) from expression trees: traverse the expression tree pre-orderly. For example, traversing the depicted arithmetic expression in pre-order yields "+ * A ? B C + D E". In prefix notation, there is no need for any parentheses as long as each operator has a fixed number of operands. Pre-order traversal is also used to create a copy of the tree.

Post-order traversal can generate a postfix representation (Reverse Polish notation) of a binary tree. Traversing the depicted arithmetic expression in post-order yields "A B C ? * D E + +"; the latter can easily be transformed into machine code to evaluate the expression by a stack machine. Post-order traversal is also used to delete the tree. Each node is freed after freeing its children.

In-order traversal is very commonly used on binary search trees because it returns values from the underlying set in order, according to the comparator that set up the binary search tree.

Implementations

Depth-first search implementation

Below are examples of stack-based implementation for pre-order, post-order and in-order traversal in recursive approach (left) as well as iterative approach (right).

Implementations in iterative approach are able to avoid the drawbacks of recursion, particularly limitations of stack space and performance issues.

Several alternative implementations are also mentioned.

Pre-order implementation

procedure preorder(node) if node = null return visit(node) preorder(node.left) preorder(node.right)

procedure iterativePreorder(node) if node = null return stack ← empty stack stack.push(node) while not stack.isEmpty() node ← stack.pop() visit(node) // right child is pushed first so that left is processed first if node.right ≠ null stack.push(node.right) if node.left ≠ null stack.push(node.left)

Post-order implementation

procedure postorder(node) if node = null return postorder(node.left) postorder(node.right) visit(node)

procedure iterativePostorder(node) if node = null return stack ← empty stack lastNodeVisited ← null while not stack.isEmpty() or node ≠ null if node ≠ null stack.push(node) node ← node.left else peekNode ← stack.peek() // if right child exists and traversing node // from left child, then move right if peekNode.right ≠ null and lastNodeVisited ≠ peekNode.right node ← peekNode.right else visit(peekNode) lastNodeVisited ← stack.pop()

In-order implementation

procedure inorder(node) if node = null return inorder(node.left) visit(node) inorder(node.right)

procedure iterativeInorder(node) if node = null return stack ← empty stack while not stack.isEmpty() or node ≠ null if node ≠ null stack.push(node) node ← node.left else node ← stack.pop() visit(node) node ← node.right

Another variant of pre-order

If the tree is represented by an array (first index is 0), it is possible to calculate the index of the next element:

procedure bubbleUp(array, i, leaf)
    k ← 1
    i ← (i - 1)/2
    while (leaf + 1) % (k * 2) ≠ k
        i ← (i - 1)/2
        k ← 2 * k
    return i

procedure preorder(array)
    i ← 0
    while i ≠ array.size
        visit(array[i])
        if i = size - 1
            i ← size
        else if i < size/2
            i ← i * 2 + 1
        else
            leaf ← i - size/2
            parent ← bubble_up(array, i, leaf)
            i ← parent * 2 + 2

Advancing to the next or previous node

The node to be started with may have been found in the binary search tree bst by means of a standard search function, which is shown here in an implementation without parent pointers, i.e. it uses a stack for holding the ancestor pointers.

procedure search(bst, key)
    // returns a (node, stack)
    node ← bst.root
    stack ← empty stack
    while node ≠ null
        stack.push(node)
        if key = node.key
            return (node, stack)
        if key < node.key
            node ← node.left    
        else
            node ← node.right
    return (null, empty stack)

The function inorderNext returns an in-order-neighbor of node, either the in-order-successor (for dir=1) or the in-order-predecessor (for dir=0), and the updated stack, so that the binary search tree may be sequentially in-order-traversed and searched in the given direction dir further on.

procedure inorderNext(node, dir, stack)
    newnode ← node.child[dir]
    if newnode ≠ null
        do
            node ← newnode
            stack.push(node)
            newnode ← node.child[1-dir]
        until newnode = null
        return (node, stack)
    // node does not have a dir-child:
    do
        if stack.isEmpty()
            return (null, empty stack)
        oldnode ← node
        node ← stack.pop()   // parent of oldnode
    until oldnode ≠ node.child[dir]
    // now oldnode = node.child[1-dir],
    // i.e. node = ancestor (and predecessor/successor) of original node
    return (node, stack)

Note that the function does not use keys, which means that the sequential structure is completely recorded by the binary search tree’s edges. For traversals without change of direction, the (amortised) average complexity is ${\mathcal {O}}(1),$ because a full traversal takes $2n-2$ steps for a BST of size $n,$ 1 step for edge up and 1 for edge down. The worst-case complexity is ${\mathcal {O}}(h)$ with $h$ as the height of the tree.

All the above implementations require stack space proportional to the height of the tree which is a call stack for the recursive and a parent (ancestor) stack for the iterative ones. In a poorly balanced tree, this can be considerable. With the iterative implementations we can remove the stack requirement by maintaining parent pointers in each node, or by threading the tree (next section).

Morris in-order traversal using threading

Main article: Threaded binary tree

A binary tree is threaded by making every left child pointer (that would otherwise be null) point to the in-order predecessor of the node (if it exists) and every right child pointer (that would otherwise be null) point to the in-order successor of the node (if it exists).

Advantages:

1. Avoids recursion, which uses a call stack and consumes memory and time.
2. The node keeps a record of its parent.

Disadvantages:

1. The tree is more complex.
2. We can make only one traversal at a time.
3. It is more prone to errors when both the children are not present and both values of nodes point to their ancestors.

Morris traversal is an implementation of in-order traversal that uses threading:

1. Create links to the in-order successor.
2. Print the data using these links.
3. Revert the changes to restore original tree.

Breadth-first search

Also, listed below is pseudocode for a simple queue based level-order traversal, and will require space proportional to the maximum number of nodes at a given depth. This can be as much as half the total number of nodes. A more space-efficient approach for this type of traversal can be implemented using an iterative deepening depth-first search.

procedure levelorder(node)
    queue ← empty queue
    queue.enqueue(node)
    while not queue.isEmpty()
        node ← queue.dequeue()
        visit(node)
        if node.left ≠ null
            queue.enqueue(node.left)
        if node.right ≠ null
            queue.enqueue(node.right)

If the tree is represented by an array (first index is 0), it is sufficient iterating through all elements:

procedure levelorder(array)
    for i from 0 to array.size
        visit(array[i])

Infinite trees

While traversal is usually done for trees with a finite number of nodes (and hence finite depth and finite branching factor) it can also be done for infinite trees. This is of particular interest in functional programming (particularly with lazy evaluation), as infinite data structures can often be easily defined and worked with, though they are not (strictly) evaluated, as this would take infinite time. Some finite trees are too large to represent explicitly, such as the game tree for chess or go, and so it is useful to analyze them as if they were infinite.

A basic requirement for traversal is to visit every node eventually. For infinite trees, simple algorithms often fail this. For example, given a binary tree of infinite depth, a depth-first search will go down one side (by convention the left side) of the tree, never visiting the rest, and indeed an in-order or post-order traversal will never visit any nodes, as it has not reached a leaf (and in fact never will). By contrast, a breadth-first (level-order) traversal will traverse a binary tree of infinite depth without problem, and indeed will traverse any tree with bounded branching factor.

On the other hand, given a tree of depth 2, where the root has infinitely many children, and each of these children has two children, a depth-first search will visit all nodes, as once it exhausts the grandchildren (children of children of one node), it will move on to the next (assuming it is not post-order, in which case it never reaches the root). By contrast, a breadth-first search will never reach the grandchildren, as it seeks to exhaust the children first.

A more sophisticated analysis of running time can be given via infinite ordinal numbers; for example, the breadth-first search of the depth 2 tree above will take ω·2 steps: ω for the first level, and then another ω for the second level.

Thus, simple depth-first or breadth-first searches do not traverse every infinite tree, and are not efficient on very large trees. However, hybrid methods can traverse any (countably) infinite tree, essentially via a diagonal argument ("diagonal"—a combination of vertical and horizontal—corresponds to a combination of depth and breadth).

Concretely, given the infinitely branching tree of infinite depth, label the root (), the children of the root (1), (2), ..., the grandchildren (1, 1), (1, 2), ..., (2, 1), (2, 2), ..., and so on. The nodes are thus in a one-to-one correspondence with finite (possibly empty) sequences of positive numbers, which are countable and can be placed in order first by sum of entries, and then by lexicographic order within a given sum (only finitely many sequences sum to a given value, so all entries are reached—formally there are a finite number of compositions of a given natural number, specifically 2^n?1 compositions of n ≥ 1), which gives a traversal. Explicitly:

1. ()
2. (1)
3. (1, 1) (2)
4. (1, 1, 1) (1, 2) (2, 1) (3)
5. (1, 1, 1, 1) (1, 1, 2) (1, 2, 1) (1, 3) (2, 1, 1) (2, 2) (3, 1) (4)

etc.

This can be interpreted as mapping the infinite depth binary tree onto this tree and then applying breadth-first search: replace the "down" edges connecting a parent node to its second and later children with "right" edges from the first child to the second child, from the second child to the third child, etc. Thus at each step one can either go down (append a (, 1) to the end) or go right (add one to the last number) (except the root, which is extra and can only go down), which shows the correspondence between the infinite binary tree and the above numbering; the sum of the entries (minus one) corresponds to the distance from the root, which agrees with the 2^n?1 nodes at depth n ? 1 in the infinite binary tree (2 corresponds to binary).

Sources

• Dale, Nell. Lilly, Susan D. "Pascal Plus Data Structures". D. C. Heath and Company. Lexington, MA. 1995. Fourth Edition.
• Drozdek, Adam. "Data Structures and Algorithms in C++". Brook/Cole. Pacific Grove, CA. 2001. Second edition.
• "Tree Transversal" (math.northwestern.edu)

External links

• Storing Hierarchical Data in a Database with traversal examples in PHP
• Managing Hierarchical Data in MySQL
• Working with Graphs in MySQL
• See tree traversal implemented in various programming language on Rosetta Code
• Tree traversal without recursion
• Tree Traversal Algorithms
• Binary Tree Traversal
• Tree Traversal In Data Structure